Improved wet splitter for micropalaeontological analysis, and assessment of uncertainty using data from splitters

Analyses of foraminiferal assemblages have often been implemented on dry samples, which are easy to split. In some cases, the wet-picking method is preferred as it allows the preservation of more foraminiferal forms and facilitates the picking of live foraminifera. However, the increased execution time needed for wet picking may cause micropalaeontologists to refrain from employing it in a routine way. Here we present an improved and cost-effective wet splitter (including a 3-D printing file) for micropalaeontological samples aimed to reduce picking time while keeping information loss to a minimum. We demonstrate small sample losses as well as statistical consistency across splits. We show that the time saved picking a subset will always be larger than the relative increase in statistical uncertainty.

1 Introduction

Splitting samples into smaller subsamples is often necessary in micropalaeontological studies. Indeed, the general high abundance of microfossils – which makes them excellent tools to reconstruct past environments – also results in very time-consuming faunal analyses. For assemblage analyses of benthic foraminifera, Patterson and Fishbein (1989) recommend a count of at least 300 specimens in order to identify the species comprising 10 % or more of an assemblage. Studies using fossil foraminifera are most often carried out on dry material; if the samples need splitting, the well-known “Otto” microsplitter (Otto, 1933) is typically used. However, in many cases it is necessary to keep the samples in a liquid, for example to reduce the risk of destroying fragile (poorly cemented) or thin-shelled forms during the drying process. Additionally, the number of studies focusing on living foraminifera is increasing, which suggests an increase in the use of wet samples. Indeed, the methods employed to distinguish live from dead foraminifera, such as the rose Bengal stain (Walton, 1952) or the more recent CellTracker^™ Green (Bernhard et al., 2006), are more efficient when the specimens are in a liquid, as the stain/labelling becomes easier to discern. Moreover, the non-fossilizing soft-shelled forms will also be preserved. Wet-picking for assemblage studies is considerably more time-consuming than comparable work using dry samples (Murray, 2006), adding to the necessity for a reliable wet splitter. A wet-splitter device was first described by Elmgren (1973) and subsequently improved by Scott and Hermelin (1993). However, the improved design by Scott and Hermelin (1993) is also suboptimal for several reasons. First, sample losses may occur due to leakage as well as by sample sticking to compartment wall edges and their crossing point (Scott and Hermelin, 1993). Second, the relatively short cylinder could potentially prevent heavy particles such as foraminifera from being homogeneously distributed in the water column before settling. Third, the off-centre drainage system results in non-symmetrical water swirls, which may bias the spatial distribution of particles between the splits. No quantitative or statistically consistent results regarding studies of these effects have been reported for the previous devices.

Here we present a modified device built at the Department of Geology, Lund University, Sweden. The main improvements are a fully hermetic and symmetric splitter design with a central drainage system and very thin, polished walls made possible by the advancement of 3-D printing techniques. For the first time, a comparison both between all the splits and with the known input sample was made, enabling the assessment of loss and inhomogeneity.

Table 1 Illustration of the increase in statistical uncertainty from estimating the total number of specimens (N) from a picked subsample (comparing the last two rows). Both the general expression and a made-up example are shown. The total number in the example is arbitrarily set to a number close to 400 for illustration purposes. The relative uncertainty is increased by √(n), while the time saved increases by n.

2 Description of the device

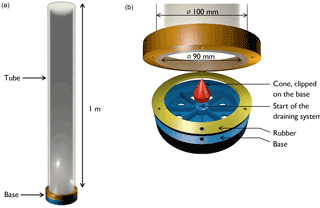
We designed a new splitter (Fig. 1) based on the one by Scott and Hermelin (1993). The device is composed of two parts: a 1 m PVC cylinder with an outside diameter of 100 mm and a plastic base created in one piece using a 3-D printer. The base is divided into eight sections with 1 cm diameter outlets hermetically sealed by rubber stoppers. To avoid particles sticking to the edges of the walls that separated the sections, the walls of the base were made as thin as possible (< 1 mm thick) with v-shaped upper edges, and the base was polished and varnished. The draining system is a siphon, composed of a PVC pipe with a diameter of 6 mm, linked to the centre of the base (Fig. 1).

There are three main innovations. Besides the novel design of the section walls, we have added a rubber ring between the base of the device and the cylinder (Fig. 1b), which considerably reduces the potential problem of leakage, as reported from previous devices (Scott and Hermelin, 1993). Six screws keep the cylinder and the base together. Furthermore, the draining pipe is connected to the midpoint of the base, symmetrizing the effect of the small swirl formed during drainage. Finally, adding a cone at the midpoint of the eight sections results in (1) preventing particles from settling in the central drainage hole, where they would be lost when the water is drained, and (2) an even distribution of the particles among the eight sections (Fig. 1b). The midpoint cone effectively reduces the area where particles could get stuck compared with previous designs.

3 Assembly and usage

To operate the splitter, the user needs to assemble the cylinder, the rubber ring, and the base and then firmly tighten the screws. After filling the cylinder with water, strong turbulence is created by stirring, ensuring an equal distribution of the particles in the water column. The user should rapidly pour the sample into the cylinder and let it settle for at least 1 h. Once the water has been slowly siphoned through the drainage pipe, the two parts of the device can be carefully separated. The rubber stoppers of the eight sections can be removed, and each split is collected into individual vials using a squeeze bottle.

4 Performance tests

The following section describes a series of tests carried out to quantify the accuracy that can be expected when using the device. The statistical uncertainties were first assessed using a statistical model and the Poisson distribution (see details in the Supplement). The existence of the established statistical model enables a quantitative interpretation of the advantage of using a splitter. If picking only a fraction 1∕n of the total sample, the time spent picking will decrease by a factor n. The Poisson distribution implies that the relative statistical uncertainty in the measurement, given by $\mathrm{1}/\surd \mathit{\mu }$, will then increase by √(n). This is shown with both the general mathematical expression and an explicit example in Table 1. This quantifies the trade-off, where the time saved on picking a subset will always be larger than the relative increase in statistical uncertainty. The acceptable level of statistical uncertainty has to be decided for the individual sample and analysis goals.

5 Sample tests: method and results

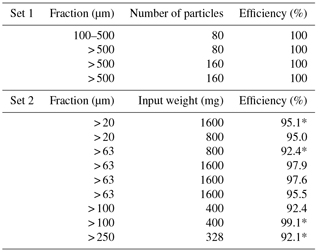
Two sets of tests were executed to assess the efficiency of the splitter. We used marine sediment samples that were sieved through different mesh screens. The efficiency (denoted by ε in Fig. 2) was defined as the fraction of the input sample recovered when summing over all splits after the splitting procedure. In order to assess whether differences between splits were statistically significant, which would indicate leaks or other inhomogeneities in the construction, a statistical uncertainty was assigned to the measurements according to the previously verified Poisson distribution fits (e.g. a measured value of 9 has an uncertainty $\surd \mathrm{9}=\mathrm{3}$). In the first set, a known number of sediment grains with sizes of 100–500 or > 500 µm was poured into the device, and then each split was picked (Table 2). In all the cases, the total number of grains was always recovered, yielding 100 % efficiency (Table 2). However, since time constraints limit counting tests to small numbers of grains, there are potentially large statistical fluctuations in such efficiency measurements, potentially hiding smaller systematic effects. Thus, in a second set, we used larger, well-sorted sediment samples with grain sizes of > 20, > 63, > 100, and > 250 µm, with a maximum grain size of 600 µm. Here, the weight of each split was measured and compared to the expected weight from the known input weight (Table 2). For all the tests, the weight measured in each split agreed with the average overall splits within statistical uncertainties (Fig. 2, solid lines), and no systematic differences between the splits were observed. The deviations from the average were verified to be normally distributed, as is expected from random fluctuations. There were small losses of sediment (Fig. 2), attributed to losses in the water and on the compartment walls. An average efficiency of 95 % was seen, and the efficiency was independent of grain size (Table 2). The absolute losses were seen to have a positive but steadily decreasing dependence on the input weight, which is interpreted as a saturation of possible losses. Where high accuracy is needed, initially performing this type of test, probing the grain size and weight dependence of the efficiency of the device, allows for corrections of the subsequently measured foraminiferal data.

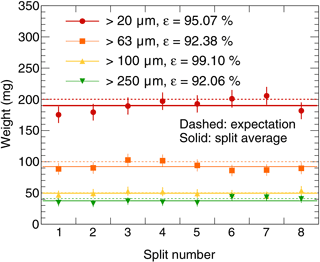
Figure 2 The weight measured in each split, compared to the expectation without losses (dashed lines) and the average across the splits in each test (solid lines) for a few representative example samples. The vertical bars on the data points represent the statistical uncertainty. The grain size and the efficiency ε for each test are given in the legend.

Table 2 Grain size, number of particles, input weight, and splitter efficiency for both the first and the second sets of tests. * tests presented in Fig. 2.

6 Conclusions

The improved wet splitter described in this paper splits samples with small sample losses and without introducing systematic differences between sample splits. Comparisons across all splits and with the known total input show that, for a range of particle sizes, picking a subset of the splits gives statistically compatible results to picking all of them. The verified statistical model used quantifies the associated larger relative statistical uncertainties from picking only a subsample. With both the time saved and increased statistical uncertainties thus known, the optimal balance can be decided on a use-case basis. Furthermore, efficiency losses are predictable, and we present a method to measure them. We recommend the use of the wet splitter to analyse foraminiferal assemblages in a more time-efficient manner.